Code coverage using a dynamic symbolic execution
by @Romain Thomas and @Jonathan Salwan - 2015-10-12
1 - Abstract
Code coverage is mainly used in the vulnerability research area. The goal is to generate inputs which will reach different parts of the program's code. Then, if an input makes the program crash, we check if the crash can be exploited or not. A lot of methods exist to perform code coverage - like random testing or mutation generation - but in this short blog post, we will focus on code coverage using a dynamic symbolic execution (DSE) and explain why it's not a trivial task. Please, note that covering up the code doesn't mean finding every possible bugs. Some bugs do not make the program crash and this talk from slides 35 to 38 explains why. However, if we perform model checking associated with code coverage, it starts to get interesting =).
2 - Code coverage and DSE
Note that unlike a SSE (static symbolic execution), a DSE is applied on a trace and can discover new branches only if these ones are reached during the execution. To go through another path, we must solve one of the last branch constraints discovered from the last trace. Then, we repeat this operation until all branches are taken.
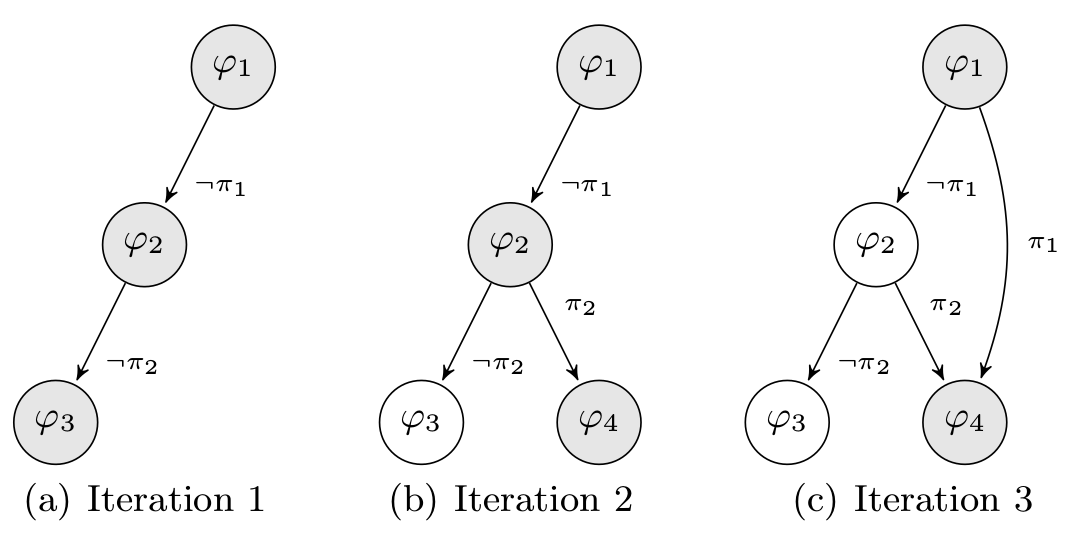
For example, let's assume a program P which takes an input called I, where I may be a model M or a random seed R. An execution is denoted P(I) and returns a set of constraints PC. All φi represent basic blocks and πi represent the branches constraint. A model Mi is (at least) one valid solution of a constraint πi. For example, M1 = Solution(¬π1 ∧ π2). To discover all paths, we maintain a worklist denoted W which is a set of M.
At the first iteration, I = R, W = ∅ and P(I) → PC. Then, ∀π ∈ PC, W = W ∪ {Solution(π)} and we execute once again the program such that ∀M ∈ W, P(M). When a model M is injected in the program's input, it is deleted from the worklist W. Then, we repeat this operation until W is empty.
Symbolic code coverage implies some pros and cons. For us, it is really useful when we work on a obfuscated binary. Indeed, applying symbolic coverage can detect opaque predicates or unreachable code but also repair a flattened graph (we will release soon another blog post about Triton and o-llvm). The worst con about the symbolic execution is when your expressions are too complexes which implies a timeout from the SMT solver or an impressive memory consumption (in the past, our bigger symbolic expression has consumed ~450 Go of RAM before timeout). This scenario mainly occurs when we analyse real large binaries or obfuscated binaries which contain polynomial functions. Some of these cons may partially be fixed by optimizing symbolic expressions but this subject will be another story to come later :).
3 - Perform code coverage using Triton
Since the version v0.1 build 633 (commit 474fe2), Triton integrates everything we need to
perform code coverage. These new features allow us to deal and compute the SMT2-Lib representation over an AST.
In the rest of the blog post, we will focus on the design and the algorithm used to perform code coverage.
3.1 - Algorithm
As an introduction (and to not turn our brain upside down), let assume this following sample of code which comes from the samples directory.
01. char *serial = "\x31\x3e\x3d\x26\x31"; 02. int check(char *ptr) 03. { 04. int i = 0; 05. while (i < 5){ 06. if (((ptr[i] - 1) ^ 0x55) != serial[i]) 07. return 1; 08. i++; 09. } 10. return 0; 11. }
Basically, this function checks if the input is equal to elite, and returns 0 if it is true, otherwise it returns 1. The control flow graph of this function is described below.
It's an interesting first example, because to cover all basic blocks we need to find the good input.
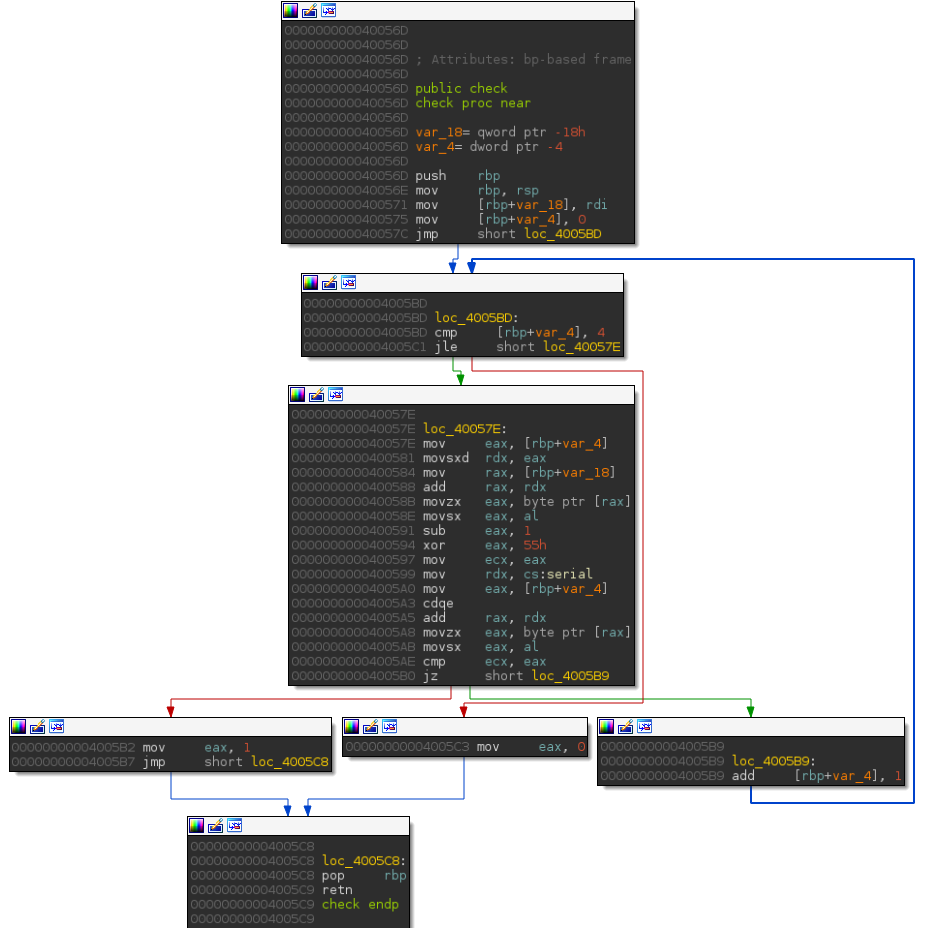
We can see that only one variable can be controlled, the one located at the address rbp+var_18 which refers to the argv[1]'s pointer.
The goal is to reach all the basic blocks in the function check by computing the constraints and using the snapshot engine until that every basic blocks are reached.
For instance, the constraint to reach the basic block located at the address 0x4005C3 is [rbp+var_4] > 4 but we do not control this variable directly.
In the other hand, the jump at the address 0x4005B0 depends on the user input and this constraint can be solved by performing a symbolic execution.
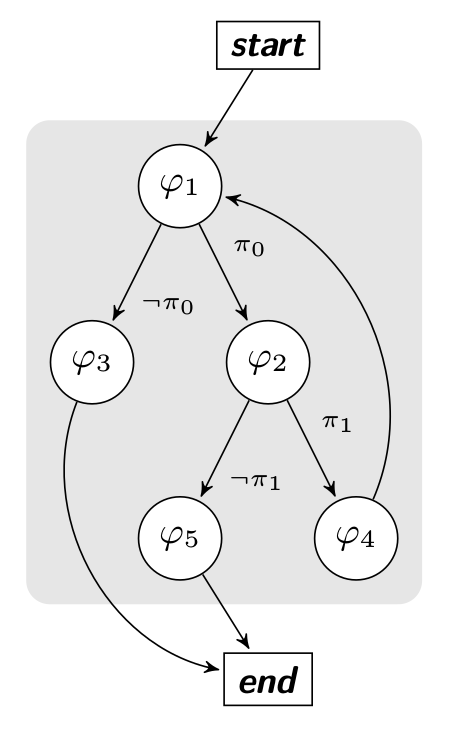
The algorithm which generalizes the previous idea is based on the Microsoft's fuzzer algorithm (SAGE)
and the next diagram represents our check function with its constraints. The start and end nodes represent respectively the function's prologue (0x40056D) and the function's epilogue (0x4005C8).
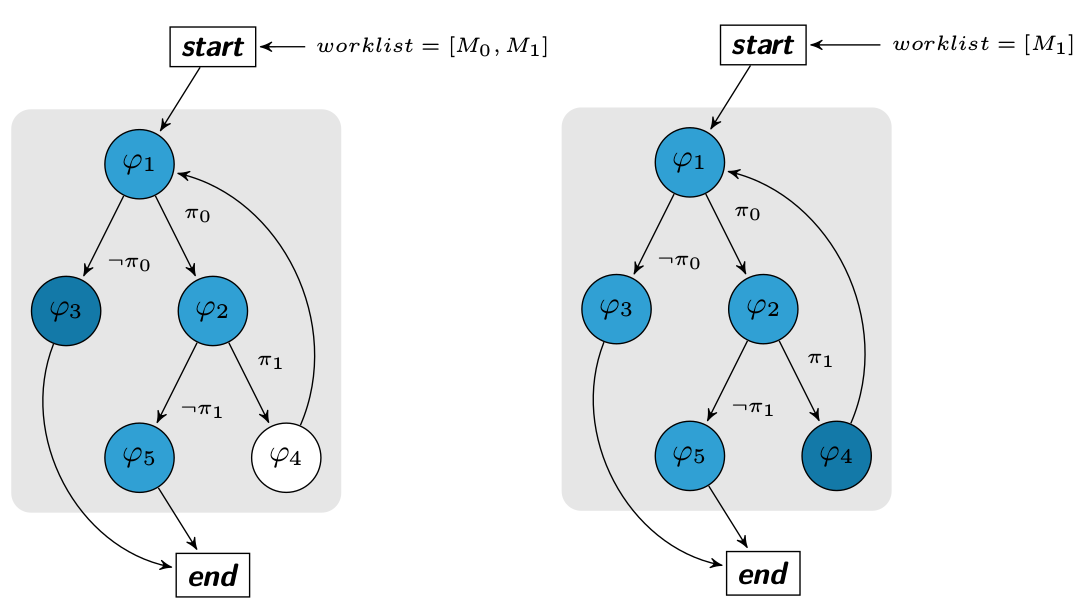
Before the first execution, we know nothing about branches' constraints. So, as explained in the previous chapter, we inject some random seeds to collect the first PC and build our set W. The trace of the first execution P(I) is represented by the basic blocks in blue.
This execution gives us our first path constraint P(I) → (π0 ∧ ¬π1).

Based on our first trace, we know that there are 2 branches (π0 ∧ ¬π1) discovered and so 2 others undiscovered. To reach the basic bloc φ3, we compute the negation of the first branch constraint. If and only if the solution Solution(¬π0) is SAT, we add the model to the worklist W.
Same for φ4 such that W = W ∪ {Solution(π0 ∧ ¬(¬π1))}. Once all solutions have been generated and models added to the worklist, we execute every models from the worklist.
3.2 - Implementation
One condition to perform code coverage, is to predict the next instruction address when we are on a jump instruction. This condition is necessary to build the path constraint.
We can not put a callback after a branch instruction because the RIP register has already changed. As Triton creates semantics expressions for all registers, the idea is to
evaluate RIP when we are on a branch instruction.
In a first time, we have developed a SMT evaluator to compute the RIP but we saw a little bit later that Pin provides
IARG_BRANCH_TARGET_ADDR and
IARG_BRANCH_TAKEN which can be used to know
the next RIP values. With Pin, computing the next address is very easy, nevertheless the SMT evaluator was useful to check instruction's semantics.
To perform the evaluation, we implemented the visitor pattern to transform the SMT abstract syntax tree (AST) to a Z3 AST. This design can be used to transform our SMT AST into any others representations.
The Z3 AST is easier to handle and can be evaluated or simplified with Z3 API. The transformation is performed by src/smt2lib/z3AST.h and src/smt2lib/z3AST.cpp.
We will now explain how the code coverage's tool works. Let's assume that inputs come from command's line. Firstly, we have:
160. def run(inputSeed, entryPoint, exitPoint, whitelist = []): 161. ... 175. if __name__=='__main__': 176. TritonExecution.run("bad !", 0x400480, 0x40061B, ["main", "check"]) # crackme_xor
At line 176, we define the input seed bad ! which is the first program's argument (argv[1]). Then, we give the address from the beginning of
the code coverage (start block) - it's at this address that we will take a snapshot.
The third argument matches with the end block - it's at this address that we will restore the snapshot.
Finally, we can set a whitelist to avoid specific functions like library's functions, cryptographic's function and so on.
134. def mainAnalysis(threadId): 135. 136. print "[+] In main" 137. rdi = getRegValue(IDREF.REG.RDI) # argc 138. rsi = getRegValue(IDREF.REG.RSI) # argv 139. 140. argv0_addr = getMemValue(rsi, IDREF.CPUSIZE.QWORD) # argv[0] pointer 141. argv1_addr = getMemValue(rsi + 8, IDREF.CPUSIZE.QWORD) # argv[1] pointer 142. 143. print "[+] In main() we set :" 144. od = OrderedDict(sorted(TritonExecution.input.dataAddr.items())) 145. 146. for k,v in od.iteritems(): 147. print "\t[0x%x] = %x %c" % (k, v, v) 148. setMemValue(k, IDREF.CPUSIZE.BYTE, v) 149. convertMemToSymVar(k, IDREF.CPUSIZE.BYTE, "addr_%d" % k) 150. 151. for idx, byte in enumerate(TritonExecution.input.data): 152. if argv1_addr + idx not in TritonExecution.input.dataAddr: # Not overwrite the previous setting 153. print "\t[0x%x] = %x %c" % (argv1_addr + idx, ord(byte), ord(byte)) 154. setMemValue(argv1_addr + idx, IDREF.CPUSIZE.BYTE, ord(byte)) 155. convertMemToSymVar(argv1_addr + idx, IDREF.CPUSIZE.BYTE, "addr_%d" % idx)
The next code being executed is the mainAnalysis callback, we inject values to the inputs selected (line 148, 154) and we convert these inputs as symbolic variables (line 149, 155).
All inputs selected are stored in a global variable called TritonExecution.input. Then, we can begin the code exploration.
58. if instruction.getAddress() == TritonExecution.entryPoint and not isSnapshotEnabled(): 59. print "[+] Take Snapshot" 60. takeSnapshot() 61. return
When we are at the entry point, we take a snapshot in order to replay code exploration with a new input.
52. if instruction.getAddress() == TritonExecution.entryPoint + 2: 53. TritonExecution.myPC = [] # Reset the path constraint 54. TritonExecution.input = TritonExecution.worklist.pop() # Take the first input 55. TritonExecution.inputTested.append(TritonExecution.input) # Add this input to the tested input 56. return
We reset the path constraint (line 53) and we pop a new input from the worklist.
63. if instruction.isBranch() and instruction.getRoutineName() in TritonExecution.whitelist: 64. 65. addr1 = instruction.getAddress() + 2 # Address next to this one 66. addr2 = instruction.getOperands()[0].getValue() # Address in the instruction condition 67. 68. # [PC id, address taken, address not taken] 69. if instruction.isBranchTaken(): 70. TritonExecution.myPC.append([ripId, addr2, addr1]) 71. else: 72. TritonExecution.myPC.append([ripId, addr1, addr2]) 73. 74. return
This test above checks if we are on a branch instruction like (jnz, jle ...) and if we are in a function which is
into the white list. If so, we get the two possible addresses (addr1 and addr2) and the effective address is
computed by isBranchTaken() (line 69).
Then, we store into the path constraint the RIP expression, the address taken and the address not taken (line 73-76).
81. if instruction.getAddress() == TritonExecution.exitPoint: 82. print "[+] Exit point" 83. 84. # SAGE algorithm 85. # http://research.microsoft.com/en-us/um/people/pg/public_psfiles/ndss2008.pdf 86. for j in range(TritonExecution.input.bound, len(TritonExecution.myPC)): 87. expr = [] 88. for i in range(0,j): 89. ripId = TritonExecution.myPC[i][0] 90. symExp = getFullExpression(getSymExpr(ripId).getAst()) 91. addr = TritonExecution.myPC[i][1] 92. expr.append(smt2lib.smtAssert(smt2lib.equal(symExp, smt2lib.bv(addr, 64)))) 93. 94. ripId = TritonExecution.myPC[j][0] 95. symExp = getFullExpression(getSymExpr(ripId).getAst()) 96. addr = TritonExecution.myPC[j][2] 97. expr.append(smt2lib.smtAssert(smt2lib.equal(symExp, smt2lib.bv(addr, 64)))) 98. 99. 100. expr = smt2lib.compound(expr) 101. model = getModel(expr) 102. 103. if len(model) > 0: 104. newInput = TritonExecution.input 105. newInput.setBound(j + 1) 106. 107. for k,v in model.items(): 108. symVar = getSymVar(k) 109. newInput.addDataAddress(symVar.getKindValue(), v) 110. print newInput.dataAddr 111. 112. isPresent = False 113. 114. for inp in TritonExecution.worklist: 115. if inp.dataAddr == newInput.dataAddr: 116. isPresent = True 117. break 118. if not isPresent: 119. TritonExecution.worklist.append(newInput) 120. 121. # If there is input to test in the worklist, we restore the snapshot 122. if len(TritonExecution.worklist) > 0 and isSnapshotEnabled(): 123. print "[+] Restore snapshot" 124. restoreSnapshot() 125. 126. return
The last step happens when we are on the exit point. Lines 84 to 120 are the SAGE implementation. In few words, we browse the path constraints' list and for each PC, we try to get the model which satisfies the negation. If there is a valid model to reach the new target basic block, we add the model into the worklist. Once all models are inserted into the worklist, we restore the snapshot and we re-inject each model as input seed.
The full code can be found here and its execution on our example looks like this:
$ ./triton ./tools/code_coverage.py ./samples/crackmes/crackme_xor abc [+] Take Snapshot [+] In main [+] In main() we set : [0x7ffd5ef8254d] = 62 b [0x7ffd5ef8254e] = 61 a [0x7ffd5ef8254f] = 64 d [0x7ffd5ef82550] = 20 [0x7ffd5ef82551] = 21 ! loose [+] Exit point {140726196774221: 101} [+] Restore snapshot [+] In main [+] In main() we set : [0x7ffd5ef8254d] = 65 e [0x7ffd5ef8254e] = 61 a [0x7ffd5ef8254f] = 64 d [0x7ffd5ef82550] = 20 [0x7ffd5ef82551] = 21 ! loose [+] Exit point {140726196774221: 101, 140726196774222: 108} [+] Restore snapshot [+] In main [+] In main() we set : [0x7ffd5ef8254d] = 65 e [0x7ffd5ef8254e] = 6c l [0x7ffd5ef8254f] = 64 d [0x7ffd5ef82550] = 20 [0x7ffd5ef82551] = 21 ! loose [+] Exit point {140726196774221: 101, 140726196774222: 108, 140726196774223: 105} [+] Restore snapshot [+] In main [+] In main() we set : [0x7ffd5ef8254d] = 65 e [0x7ffd5ef8254e] = 6c l [0x7ffd5ef8254f] = 69 i [0x7ffd5ef82550] = 20 [0x7ffd5ef82551] = 21 ! loose [+] Exit point {140726196774224: 116, 140726196774221: 101, 140726196774222: 108, 140726196774223: 105} [+] Restore snapshot [+] In main [+] In main() we set : [0x7ffd5ef8254d] = 65 e [0x7ffd5ef8254e] = 6c l [0x7ffd5ef8254f] = 69 i [0x7ffd5ef82550] = 74 t [0x7ffd5ef82551] = 21 ! loose [+] Exit point {140726196774224: 116, 140726196774225: 101, 140726196774221: 101, 140726196774222: 108, 140726196774223: 105} [+] Restore snapshot [+] In main [+] In main() we set : [0x7ffd5ef8254d] = 65 e [0x7ffd5ef8254e] = 6c l [0x7ffd5ef8254f] = 69 i [0x7ffd5ef82550] = 74 t [0x7ffd5ef82551] = 65 e Win [+] Exit point [+] Done !
3.3 - Further improvement
Currently, the evaluator is quite slow and we loose a lot of time to evaluate expressions. One feature that should improve the evaluator speed is a SMT simplifier. We plan to develop a passes system (like LLVM) to simplify the SMT tree.
The goal is to register some expressions transformation rules before sending expressions to the evaluator or the solver. For example, that's what miasm2 already does.
There are a lot of mini tricks to lighten symbolic expressions which are easy to implement and really beneficial. For example,
the transformation of the expression rax1 = (bvxor rax0 rax0) → rax1 = (_ bv64 0) will break the rax's symbolic
expression chain.
4 - Conclusion
Although the code coverage using a symbolic resolution is a nice way to cover a code without guessing the inputs, it's clearly not a trivial task. The paths explosion implies the memory consumption and in several cases the expressions are too complex to be computed but this method remains truly effective on short parts of code.
Free note: To improve the symbolic coverage, it could be interesting to deal with bits-flip/random seeds when expressions are too complex or to deal with symbolic execution and abstract domains.